Зі стереометрії відомо умова перпендикулярності двох площин: якщо площина проходить через перпендикуляр до даної площини (або паралельна цьому перпендикуляру), вона перпендикулярна до даної площині.

Через цю точку А можна провести безліч площин перпендикулярних даній площині Р (рис. 3.19). Ці площини утворюють у просторі пучок площин, віссю якого є перпендикуляр АВ, опущений з точки на площину Р.

На епюрі (рис. 3.20) показано побудову однієї з площин цього пучка. Насамперед через проекції точки А проведені проекції перпендикуляра АК до даної площини. Побудова А 1 До 1 і А 2 До 2 не викликає труднощів, оскільки площина Р задана основними лініями. Потім проекції тієї ж точки А проведені проекції довільної лінії АD. Ці дві лінії, що перетинаються АК і АD і визначають шукану площину Р.

Приклади позиційних та метричних завдань на площину

Приклад 1 . У площині, заданій трикутником АВС, побудувати точку D (рис. 3.21).

Рішення.

1. Необхідно у цій площині провести пряму. Задамо для цього дві точки, що свідомо лежать у даній площині. Однією з таких точок може бути вершина А(А1; А2) трикутника. Другу точку Е(Е 1 ;Е 2) поставимо на стороні ВС. Через однойменні проекції А 1 та Е 1 , А 2 та Е 2 проведемо прямі. Ці прямі є проекціями прямої. Що лежить у цій площині.

2. На побудованій прямій АЕ задаємо точку D. Для цього побудуємо D 1 ÎА 1 Е 1 і D 2 ÎА 2 Е 2 . Точка D лежить у заданій площині, тому що вона належить прямій АЕ, що лежить у цій площині

Приклад 2 . Побудувати лінію найбільшого ухилу площини, заданої паралельними прямими а(а 1 ; а 2) та b(b 1 ; b 2) та визначити кут a між цією площиною та горизонтальною площиною проекцій (рис. 3.22)

Рішення

1. Проведемо горизонталь h цієї площини (див. гл.3 рис. 3.3, в). Проекціями цієї горизонталі будуть прямі h1 і h2.
2. Проведемо пряму, перпендикулярну до горизонтальної проекції горизонталі, та відзначимо точки С 1 - перетину її з h 1 D 1 – са 1 . Пряма 1 D 1 є горизонтальною проекцією лінії найбільшого ската.
3. Побудуємо фронтальні проекції З 2 та D 2 . Для цього з 1 і D 1 проведемо вертикальні лінії зв'язку до перетину відповідно з h 2 і а 2 .
4. Пряма, що з'єднує точки З 2 і D 2 є фронтальною проекцією лінії найбільшого ухилу.
5. Кут a визначаємо з прямокутного трикутника D 1 C 1 E 0 побудованого на З 1 D 1 як на катете. Другий катет D0D1 = E2D2. Шуканий кут a=ÐD 0 C 1 D 1

Приклад 3 . Задана площина прямими АВ і CD, що перетинаються. Визначити, чи лежить пряма KL у цій площині.

Рішення.

1. Позначимо точки перетину фронтальних проекцій прямих АВ та KL через 1 2 і прямих CD та KL через 2 2 .

2. Будуємо їх горизонтальні проекції – точки 11 і 22 на горизонтальній проекції (K1L1) прямої KL. З побудови видно, що точки 1(1112) і 2(2122) пряма KL на заданій площині не лежать. Отже, пряма KL у площині не лежить. Розв'язання цього завдання можна розпочати і з перетину горизонтальних проекцій.

Приклад 4 . У площині, заданій двома паралельними прямими АВ та CD, провести фронталь на відстані 15 мм від фронтальної площини проекцій (рис. 3.24)

Рішення. Проводимо на відстані 15 мм від осі проекцій паралельну їй горизонтальну проекцію (1 1 -2 2) фронталі, яка перетинає прямі А 1 В 1 і C 1 D 1 у точках 1 1 і 2 2 .

Потім знаходимо точки 1 1 і 2 2 на прямих А 2 2 і C 2 D 2 і проводимо через них фронтальну проекцію (1 2 2 2) фронталі.

Приклад 5 . Знайти пряму перетину площин Р і Q.

Рішення. Площина Р і Q перетинаються по прямій загального положення, що проходить через точку-слід (М 1; М 2) перетину горизонтальних слідів площин. Точка-слід (N 1 ;N 2) перетину фронтальних слідів площин недоступна, т.к. ці сліди площин за завданням, у межах креслення не перетинаються.

Замість точки (N 1 ;N 2) необхідно знайти іншу довільну точку прямої перетину, загальну для заданих площин. Для цього вводимо допоміжну площину R, наприклад паралельну П, яка, як відомо, перетинає кожну з даних площин по горизонталі. На їхньому перетині отримуємо допоміжну точку (К 1 ;К 2), загальну для даних площин. Знайшовши цю другу точку (К 1 ;К 2) прямий, проводимо її проекцію: горизонтальну через точки М 1 і К 1 і фронтальну через точки М 2 і К 2 .

Приклад 6 . Знайти точку перетину прямої АВ із площиною Р (рис. 3.26)

Рішення. Позначимо шукану точку через точку К. Оскільки точка К (К 1 ;К 2) лежить на профільно-проецірующій площині. То її профільна проекція (К3) повинна лежати на профільному сліді (Р3) площині. Разом з тим, оскільки ця ж точка лежить і на прямій АВ, то її профільна проекція (К 3) повинна лежати десь на профільній проекції (А 3 В 3) прямий. Отже, шукана точка повинна лежати на їх перетині. Знайшовши профільний слід площини та профільну проекцію прямої, отримуємо на їх перетині профільну проекцію (К 3) точки, що шукається. Знаючи профільну проекцію (До 3) шуканої точки, знаходимо дві інші її проекції на однойменних проекціях прямої.

Приклад 7 . Дані площину Р і точка А. Визначити відстань точки до площини (рис. 3.27)

Рішення. Опускаємо з точки А (А 1; А 2) перпендикуляр на площину Р і знаходимо його основу на цій площині, для чого шукаємо точку К (К 1 ; К 2) перетину перпендикуляра з площиною. Маючи проекції (А 1 К 1; А 2 К 2) відрізка перпендикуляра, визначимо його дійсну величину методом прямокутного трикутника.

Приклад 8 . Дано трикутник АВС і точка К. Визначити відстань між ними. (Рис. 3.28)

Рішення. Опускаємо із заданої точки Е (Е 1 ;Е 2) перпендикуляр на площину трикутника: К 1 Е 1 перпендикулярно горизонтальній проекції горизонталі (К 1 Е 1 ^С 1 F 1), К 2 Е 2 перпендикулярно фронтальної проекції фронталі (К 2 Е 2 ^А 2 D 2). Знаходимо точку перетину перпендикуляра з площиною трикутника (К 1 ;К 2) , визначаємо натуральну величинувідрізка перпендикуляра (К 1 Е 1; К 2 Е 2) методом прямокутного трикутника.

Розділ 4

Методи перетворення комплексного креслення (епюра Монжа)

Перпендикулярність площин Визначення. Дві площини називаються перпендикулярними, якщо лінійний кут при ребрі двогранного кута між цими площинами - прямий.
Ознакаперпендикулярність площин.Якщо площина проходить через пряму, перпендикулярну до іншої площини, то ці площини перпендикулярні.
Доказ. Нехай aі? - дві площини, що перетинаються, з- пряма їх перетину та а- Пряма перпендикулярна площині? і лежить у площиніa. А - точка перетину прямихaі с.У площині? з точки А відновимоперпендикуляр, і нехай це буде пряма b. Пряма аперпендикулярнаплощині? , а значить вона перпендикулярна і будь-який прямий у цій площині, тобто прямі bі зперпендикулярні . Кут між прямими аі Ь -лінійний площинами aі? і дорівнює він 90 °, такяк пряма аперпендикулярна до прямоїb(Підказаному).aі? перпендикулярні.

Теорема 1. Якщо з точки, що належить одній з двох перпендикулярних площин, провестиперпендикуляр до іншої площині, це перпендикуляр повністю лежить у першій площині.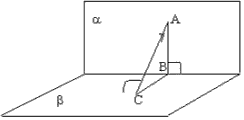
Доказ. Нехай aі? - перпендикулярні площини та з -пряма їх перетину, А - точкалежачаплощини aі не належить прямою с.Нехай перпендикуляр до площини? проведений з точки А , не лежить у площині a, Тоді точка С - основа цього перпендикуляра лежить уплощині? і не належить прямий с.З точки А опустимо перпендикуляр АВ безпосередньо с.Пряма АВ перпендикулярнаплощині (використовую теорему 2).Через пряму АВ та точку Спроведемо площину? (Пряма і точка визначають площину, причому тільки одну). Ми бачимо, що вплощині ? з однієї точки А на прямуВС проведено два перпендикуляри, чого бути не може, значить пряма АСзбігається з прямою АВ, а пряма АВ у свою чергу повністю лежить у площині a.

Теорема 2. Якщо в одній із двох перпендикулярних площин провести перпендикуляр до їхньої лініїперетину, цей перпендикуляр буде перпендикулярний другій площині.
Доказ. Нехай aі? - дві перпендикулярні площині, з -пряма їх перетину та а -пряма перпендикулярна до прямої зі лежить у площиніa. А - точка перетину прямих аі с.У площині? з точки А відновимо перпендикуляр, і нехай це буде пряма b.Кут між прямими аіb- Лінійний кут при ребрі двогранного кута міжплощинами aі? і дорівнює він 90°, тому що площиніaі? перпендикулярні. Пряма аперпендикулярна до прямоїb(за доведеним) та прямий зза умовою.Значить пряма аперпендикулярна площині? (

Визначення.Двогранним кутом називається фігура, утворена прямою а та двома напівплощинами із загальною межею а, і не належать одній площині.

Визначення.Градусною мірою двогранного кута називається градусний захід будь-якого з його лінійних кутів.

Визначення.Дві площини, що перетинаються, називаються перпендикулярними, якщо кут між ними дорівнює 90 o .

Ознака перпендикулярності двох площин.

Властивості.

1. У прямокутному паралелепіпеді всі шість граней є прямокутниками.
2. Всі двогранні кути прямокутного паралелепіпеда є прямими.
3. Квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірів.

Завдання та тести на тему "Тема 7. "Двогранний кут. Перпендикулярність площин "."

• Двогранний кут. Перпендикулярність площин
• Перпендикулярність прямої та площини - Перпендикулярність прямих та площин 10 клас

  Уроків: 1 Задань: 10 Тестів: 1

• Перпендикуляр та похилі. Кут між прямою та площиною - Перпендикулярність прямих та площин 10 клас

  Уроків: 2 Задань: 10 Тестів: 1

• Паралельність площин - Паралельність прямих та площин 10 клас

  Уроків: 1 Задань: 8 Тестів: 1

• Перпендикулярні прямі - Початкова геометрична інформація 7 клас

  Уроків: 1 Задань: 17 Тестів: 1

Матеріал теми узагальнює та систематизує відомі Вам із планиметрії відомості про перпендикулярність прямих. Вивчення теорем про взаємозв'язок паралельності та перпендикулярності прямих і площин у просторі, а також матеріал про перпендикуляр і похилих доцільно поєднувати із систематичним повторенням відповідного матеріалу з планіметрії.

Вирішення практично всіх завдань на обчислення зводяться до застосування теореми Піфагора та наслідків із неї. У багатьох завданнях можливість застосування теореми Піфагора або наслідків з неї обґрунтовується теоремою про три перпендикуляри або властивості паралельності та перпендикулярності площин.

Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих двох площин, перетинає їх по перпендикулярним прямим (див. малюнок).

Будь-яка площина, перпендикулярна до прямої перетину перпендикулярних площин, перетинає їх по перпендикулярних прямих.

Ознака перпендикулярності площин

Теорема 1. Якщо площина проходить через пряму, перпендикулярну до іншої площини, ці площини перпендикулярні (див. малюнок).

Теорема 2. Якщо пряма, що лежить в одній із двох перпендикулярних площин, перпендикулярна до лінії їх перетину, то вона перпендикулярна і до другої площини (див. рисунок).

Приклад застосування теореми 2
Нехай є дві перпендикулярні площини і , які перетинаються прямою a(Див. малюнок). Знайти відстань від точки A, що лежить у площині і не лежить у площині , площині .

У площині будуємо перпендикуляр до aчерез точку A. Нехай він перетинає aу точці B. AB- Відстань, що шукається.
Зверніть увагу на таке.
1. Через точку поза площиною можна провести безліч площин, перпендикулярних до цієї площини (див. рисунок). (Але вони пройдуть через перпендикулярну до цієї площині пряму, яка проходить через цю точку.)

2. Якщо площина перпендикулярна до даної площини, це не означає, що вона перпендикулярна і до довільної прямої, паралельної цій площині.
Наприклад, на малюнку нижче , і перетинаються прямою b, причому aвходить в одній із площин і . Отже, пряма aводночас паралельна двом перпендикулярним площинам.

Розглядається відношення перпендикулярності площин - одне з найважливіших і найбільш використовуваних у геометрії простору та її додатках.

З усієї різноманітності взаємного розташування

Двох площин особливої ​​уваги і вивчення заслуговує на те, при якому площини перпендикулярні один одному (наприклад, площини суміжних стін кімнати,

забору та ділянки землі, двері та підлоги тощо (рис. 417, а–в).

Наведені приклади дозволяють побачити одну з основних властивостей відношення, яке ми вивчатимемо, - симетричність розташування кожної з площин щодо іншої. Симетрія забезпечується тим, що поверхні начебто «соткани» з перпендикулярів. Спробуймо уточнити ці спостереження.

Нехай маємо площину α і пряму з нею (рис. 418, а). Проведемо через кожну точку прямої з прямі перпендикулярні площині α. Усі ці прямі паралельні між собою (чому?) і становлять на підставі задачі 1 § 8 деяку площину β (рис. 418, б). Природно назвати площину β перпендикулярнийплощині.

У свою чергу, всі прямі, що лежать у площині α і перпендикулярні до прямої с , утворюють площину α і перпендикулярні до площини β (рис. 418, в). Справді, якщо а - довільна така пряма, вона перетинає пряму з у певній точці М . Через точку М проходить у площині β перпендикулярна α пря-ма b , тому b а . Отже, а с, а b тому а β. Таким чином, площина α перпендикулярна площині β, а пряма є лінією їх перетину.

Дві площини називаються перпендикулярними, якщо кожна з них утворена прямими, перпендикулярними до другої площини і проходять через точки перетину цих площин.

Перпендикулярністьплощин αіβпозначається звичним уже знаком: αβ.

Одну з ілюстрацій цього визначення можна уявити, якщо розглянути фрагмент кімнати дачного будиночка(Рис. 419). У ньому підлога і стіна складені з дощок, перпендикулярних відповідно стіні та підлозі. Тому вони перпендикулярні. На практиці

це означає, що підлога горизонтальна, а стіна вертикальна.

Наведене визначення важко використовувати за фактичної перевірки перпендикулярності площин. Але якщо уважно проаналізувати міркування, що призвели до цього визначення, то бачимо, що перпендикулярність площин α та β забезпечила наявність у площині β прямої b , перпендикулярної площині α (рис. 418, в). Ми дійшли до ознаки перпендикулярності двох площин, яка найчастіше застосовується на практиці.

406 Перпендикулярність прямих та площин

Теорема 1 (ознака перпендикулярності площин).

Якщо одна з двох площин проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.

 Нехай площина β проходить через пряму b , перпендикулярну площині α та с - лінія перетину площин α та β (рис. 420, а). Усі прямі площини β, паралельні прямий b і перетинають пряму , разом із прямою b утворюють площину β. По теоремі про дві паралельні прямі, одна з яких перпендикулярна до площини (теорема 1 § 19), всі вони разом з прямою b перпендикулярні до площини α. Тобто площина β складається з прямих, що проходять через лінію перетину площин α та β та перпендикулярних до площини α (рис. 420, б).

Тепер у площині через точку А перетину прямих b і з проведемо пряму а , перпендикулярну до прямої с (рис. 420, в). Пряма а перпендикулярна до площини β, за ознакою перпендикулярності прямої та площини (а с , за побудовою, а b , тому що b α). Повторивши попередні міркування, отримаємо, що площина складається з прямих, перпендикулярних площині, що проходять через лінію перетину площин. Відповідно до визначення, площини α та β перпендикулярні. ■

Наведена ознака дає можливість встановлювати перпендикулярність площин або забезпечувати її.

П р і м е р 1 . Прикріпити щит до стовпа так, щоб він був розташований вертикально.

 Якщо стовп стоїть вертикально, достатньо докласти довільно щит до стовпа і закріпити його (мал. 421, а). Згідно з розглянутою вище ознакою, площина щита буде перпендикулярна поверхні землі. У цьому випадку завдання має безліч рішень.

Перпендикулярність площин

Якщо ж стовп стоїть похило до землі, достатньо до стовпа прикріпити вертикальну рейку (мал. 421, б), а потім щит прикріпити і до рейки, і до стовпа. У цьому випадку положення щита буде цілком визначеним, оскільки стовп та рейка визначають єдину площину. ■

У попередньому прикладі «технічне» завдання звелося до математичного завдання про проведення через цю пряму площину, перпендикулярну до іншої площини.

П р і м е р 2 . З вершини A квадрата ABCD проведено перпендикулярний його площині відрізок AK, AB = AK = а.

1) Визначити взаємне розташування площин AKC та ABD ,

AKD та ABK.

2) Побудувати площину, що проходить через пряму BD перпендикулярно до площини ABC.

3) Провести через середину F відрізка KC площину, перпендикулярну до площини KAC .

4) Знайти площу трикутника BDF.

 Побудуємо малюнок, який відповідає умові прикладу (рис. 422).

1) Площини AKC та ABD перпендикулярні, за ознакою перпендикулярності площин (теорема 1): AK ABD , за умовою. Площини AKD і ABK також перпендику-

лярні, за ознакою перпендикулярності площин (теорема 1). Дійсно, пряма AB , через яку проходить площину ABK , перпендикулярна до площини AKD , за ознакою перпендикулярності прямої та площини (теорема 1 § 18): AВ AD , як суміжні сторони квадрата; AВ AK , так як

AK ABD.

2) За ознакою перпендикулярності площин, для шуканої побудови достатньо через деяку точку прямої BD провести

408 Перпендикулярність прямих та площин

пряму, перпендикулярну до площини ABC. А для цього достатньо через цю точку провести пряму, паралельну прямій AK.

Дійсно, за умовою, пряма AK перпендикулярна до плоскості ABC і тому, згідно з теореми про дві паралельні пря-

мих, одна з яких перпендикулярна площині (теорема 1 § 19),

побудована пряма перпендикулярна площині ABC.

Побудова.

Через точку

B проводимо

ВЕ,

паралельну

(Рис. 423). Площина BDE – шукана.

3) Нехай F – середина відрізка KC. Про-

ведемо через точку

перпендику-

площині

Цій прямій бу-

дет пряма

FO , де

О - центр квадрата

ABCD (рис. 424). Дійсно, FO || AK

як середня

лінія трикутника

Оскільки

перпендикуляр-

на площині

пряма FO

бу-

дет їй перпендикулярна, по теоремі про

двох паралельних прямих, одна з кото-

рих перпендикулярна до площини (теорема 1

§ 19). Тому

FO DB. А оскільки AC DB, то DB AOF (або

KAC). Площина

BDF проходить через пряму, перпендикуляр-

ну площину KAC, тобто вона є шуканою.

4) У трикутнику

BDF відрізок FO

Висота, проведена до

стороні BD (див. мал. 424). Маємо: BD =

2 a як діагональ квад-

рата; FO = 1

AK =

1 a , за якістю середньої лінії трикутника.

Таким чином, S = 2 BD FO =

2 2 a

2 a =

. ■

Відповідь: 4)

a 2 .

Дослідження властивостей відношення перпендикуляр-

ності площин і його застосувань почнемо з про-

тієї, але дуже корисної теореми.

Теорема 2 (про перпендикуляр до лінії перетину перпендикулярних площин).

Якщо дві площини перпендикулярні, то пряма, що належить до однієї площини і перпендикулярна до лінії перетину цих площин, перпендикулярна до другої площини.

 Нехай перпендикулярні площині

α і β перетинаються по прямій с, а пряма b у площині β перпендикулярна до прямої с і перетинає її в точці В (рис. 425). За визна-

поділу перпендикулярності площин, в площині через точку В проходить пряма

b 1 перпендикулярна площині α. Зрозуміло, що вона перпендикулярна до прямої с . Але че-

рез точку прямої в площині можна провести лише одну пряму, перпендикулярну до цієї прямої. Тому

прямі b та b 1 збігаються. А це означає, що пряма однієї площини, перпендикулярна лінії перетину двох перпендикулярних площин, перпендикулярна до другої площини. ■

Застосуємо розглянуту теорему до обґрунтування ще однієї ознаки перпендикулярності площин, важливої ​​з точки зору подальшого вивчення взаємного розташування двох площин.

Нехай площини і перпендикулярні, пряма с - лінія їх перетину. Через довільну точку А прямий з проведемо

у площинах α та β прямі а та b, перпендикулярні до прямої с (рис. 426). По теоре-

ме 2, прямі а і b перпендикулярні відповідно до площин β і α, тому вони перпендикулярні між собою: а b . Пря-

а і b визначають деяку площину γ. Лінія перетину з площин α та β

перпендикулярна площині γ, за ознакою перпендикулярності прямої та площини (теорема 1 § 18): с а , с b , а γ, b γ. Якщо врахувати довільність вибору точки А на прямій з і той факт, що через точку А прямий з проходить єдина площина, їй перпендикулярна, то можна зробити такий висновок.

Теорема 3 (про площину, перпендикулярну лінію перетину перпендикулярних площин).

Площина, перпендикулярна до лінії перетину двох перпендикулярних площин, перетинає ці площини по перпендикулярним прямим.

Таким чином, встановлено ще одну властивість перпендикулярних площин. Ця властивість є характеристичною, тобто якщо вона справедлива для деяких двох площин, то площини перпендикулярні між собою. Маємо ще один ознака перпендикулярності площин.

Теорема 4 (друга ознака перпендикулярності площин).

Якщо прямі перетину двох площин третьою площиною перпендикулярної лінії їх перетину перпендикулярні, то дані площини теж перпендикулярні.

 Нехай площини α і β перетинаються по прямій з , і площина γ, перпендикулярна до прямої з , перетинає площини α і β соот-

ветственно по прямих а і b (рис. 427). За умовою, а b . Оскільки γ с , то с. А тому пряма а перпендикулярна до плоскості β, за ознакою перпендикулярності прямої та площини (теорема 1 § 18). Звідси-

так випливає, що площини α і β перпендикулярні, за ознакою перпендикулярності площин (теорема 1). ■

Заслуговують на увагу і теореми про зв'язки перпендикулярності двох площин третьої площини з їх взаємним розташуванням.

Теорема 5 (про лінію перетину двох площин, перпендикулярних третьої площини).

Якщо дві площини, перпендикулярні до третьої площини, перетинаються, то лінія їх перетину перпендикулярна цій площині.

 Нехай площини α і β, перпендикулярні до площини γ, перетинаються по прямій а (a || γ), і А - точка перетину прямої а с

Перпендикулярність площин
площиною (рис. 428). Крапка А належить-
жит лініям перетину площин γ і α, γ
і β, а, за умовою, α γ та β γ. Тому, за
визначенню перпендикулярності плоскос-
тій, через точку А можна провести прямі,
що лежать у площинах α	і β і перпендику-
лярні площини. Бо через точку
можна провести лише одну пряму, пер-
пендикулярну площину, то побудовані
прямі збігаються і збігаються з лінією
перетину площин α та β. Таким чином, пряма а - лінія
перетину площин α і β - перпендикулярна площині γ. ■

Розглянемо теорему, що описує зв'язок між паралельністю та перпендикулярністю площин. Відповідний результат ми вже мали для прямих та площин.

Теорема 6 (про паралельні площини, перпендикулярні третій площині).

Якщо одна з двох паралельних площин перпендикулярна до третьої, то і друга площина перпендикулярна їй.

 Нехай площини α та β паралельні, а площина γ перпендикулярна на площині α. Оскільки площина?

перетинає площину α, то вона повинна перетинати і паралельну їй площину β. Візьмемо у площині α про-

довільну пряму m , перпендикулярну площині γ, і проведемо через неї, а також через довільну точку площини β, площину δ (рис. 429).

Площини δ і β перетинаються по прямій п, а оскільки α∑β, то т║п (теорема 2 §18). З теореми 1 випливає, що п γ, тому перпендикулярної площини γ буде і площина β, що проходить через пряму п. ■

Доведена теорема дає ще одну ознаку перпендикулярності площин.

Через задану точку провести площину, перпендикулярну даній, можна за допомогою ознаки перпендикулярності площин (теорема 1). Достатньо через цю точку провести пряму, перпендикулярну даній площині (див. задачу 1 § 19). А потім через побудовану пряму провести площину. Вона буде перпендикулярною даної площини по зазначеною ознакою. Зрозуміло, що таких площин можна провести безліч.

Більш змістовним є завдання про побудову площини, перпендикулярної даній, за умови, що вона проходить через цю пряму. Зрозуміло, що якщо ця пряма перпендикулярна даній площині, то таких площин можна побудувати безліч. Залишилося розглянути випадок, коли ця пряма не перпендикулярна даній площині. Можливість такої побудови обґрунтована на рівні фізичних моделей прямих та площин у прикладі 1.

Задача 1 . Довести, що через довільну пряму, не перпендикулярну площині можна провести площину, перпендикулярну даній площині.

 Нехай дані площину α і пряма l, l B\ a. Візьмемо на прямій l довільну точку М і проведемо через неї пряму т, перпендикулярну до площини α (рис. 430, а). Оскільки, за умовою, l не перпендикулярна α, то прямі l і т перетинаються. Через ці прямі можна провести площину β (рис. 430, б), яка, згідно з ознакою перпендикулярності площин (теорема 1), буде перпендикулярною площині α. ■

П р і м е р 3 . Через вершину А правильної піраміди SABC з основою ABC провести пряму перпендикулярну площині бічної грані SBC.

 Для вирішення цього завдання скористаємося теоремою про перпендикуляр до лінії перетину перпендикулярних площин

(Теорема 2). Нехай K – середина ребра BC (рис. 431). Площини AKS та BCS перпендикулярні, за ознакою перпендикулярності площин (теорема 1). Справді, ВС SK та ВС АK , як медіани, проведені до основ у рівнобедрених трикутниках. Тому, за ознакою перпендикулярності прямої та площини (теорема 1 §18), пряма ВС перпендикулярна до площини AKS. Площина BCS проходить через пряму перпендикулярну площині AKS.

Побудова. Проведемо в площині AKS з точки A пряму AL, перпендикулярну до прямої KS - лінії перетину площин AKS і BCS (рис. 432). По теоремі про перпендикуляр до лінії перетину перпендикулярних площин (теорема 2), пряма AL перпендикулярна площині BCS. ■

	Контрольні питання
	На рис. 433 зображено квадрат ABCD ,
	пряма MD перпендикулярна до площини
	ABCD. Які з пар площин не є-
	ються перпендикулярними:
		MAD та MDC;		МВС та МАВ;
		ABC та MDC;		MAD і МАВ?

2. На рис. 434 зображено правило- ная чотирикутна піраміда

SABCD, точки P, M, N - середи -

ни ребер AB, BC, BS, O - центр основи ABCD. Які з пар плос- кісток перпендикулярні:

1) ACS та BDS; 2) MOS та POS;

3) COS та MNP; 4) MNP та SOB;

5) CND та ABS?

		Перпендикулярність прямих та площин
3. На рис. 435	зображено прямокутний
трикутник		з прямим кутом C та
пряма BP , перпендикулярна плоскос-
ти ABC. Які з наступних пар плос-
кісток перпендикулярні:
1) CBP та ABC;		2) ABP та ABC;

3) PAC та PBC; 4) PAC та PAB?

4. Дві площини перпендикулярні. Чи можна через довільну точку однієї зїх провести пряму в цій площині, другий площині?

5. У площині α не можна провести пряму площину β. Чи можуть ці площини бути ми?

6. Через деяку точку площини α проходить ця площина і перпендикулярна до площини, чи площини α і β перпендикулярні?

Секція паркану прикріплена до вертикального стовпа Чи стверджувати, що площина паркану вертикальна?

Як до рейки, паралельної поверхні землі, вертикально прикріпити щит?

Чому поверхня дверей, незалежно від того, зачинені вони або відчинені, розташовується вертикально до підлоги?

Чому виска щільно прилягає до вертикальної стіни, а до похилої - не обов'язково?

Чи можна до похилого стовпа прикріпити щит так, щоб він був перпендикулярний поверхні землі?

Як на практиці встановити, чи перпендикулярна площина

стіни поверхні підлоги? перпендикулярнийперпендикулярнийперпендикулярний- Пряма, лежачи - β. Правильно 7. . Можна 8.9.10.11.12.

Графічні вправи

1. На рис. 436 зображено куб ABCDA 1 B 1 C 1 D 1 .

1) Вкажіть площини, перпендикулярні до площиниВДД 1 .

2) Як розташовані площини та

A1 B1 CAB 1 C 1

Перпендикулярність площин
			437 площини квадратів ABCD та
	ABC1 D1		перпендикулярні. Відстань		СC1
	і b . Знайдіть довжину відрізка:
		АВ;		D1 C;
		D1 D;		C1 D.	дан-
	Побудуйте малюнок за наведеними
	1) Площини рівносторонніх трикутників
	АВС та АВK перпендикулярні.
		Площина АВС перпендикулярна площин BDC і BEA.
		Площини α і β перпендикулярні площині γ і пересі-
	каються по прямій а, лініями їх перетину з площиною γ
	є прямі b та с.
		У прямокутному паралелепіпеді ABCDA 1 B 1 C 1 D 1 плос-
	кістки АВ 1 З 1 та ВСА 1 перпендикулярні.

421. Відрізок OS проведений із центру О квадрата ABCD перпендикулярно до його площини.

1°) Визначте взаємне розташування площин ACS

та АВС.

2°) Визначте взаємне розташування площин ACS

та BDS.

3) Побудуйте площину, що проходить через пряму OS перпендикулярно площині ABS.

4) Побудуйте площину, перпендикулярну до площини АВС і проходить через середини сторін AD і CD.

422. З точки перетину O діагоналей ромба ABCD проведено перпендикулярний площині ромба відрізок OS; AB = DB =

1°) Визначте взаємне розташування площин SDB та

ABC, SDB та ACS.

2°) Побудуйте площину, що проходить через пряму BC перпендикулярно до площини ABD.

3) Проведіть через середину F відрізка CS площину, перпендикулярну до площини АВС.

4) Знайдіть площу трикутника BDF.

423. Даний куб ABCDA1 B1 C1 D1 .

1°) Визначте взаємне розташування площин АВ 1 С 1

та CDD1 .

2°) Визначте взаємне розташування площин АВ 1 С 1

та CD1 A1 .

3°) Побудуйте площину, що проходить через точку А перпендикулярно площині BB 1 D 1 .

4) Побудуйте перетин куба площиною, що проходить через середину ребер А 1 D 1 і B 1 C 1 перпендикулярно до площини АВС. 5) Визначте взаємне розташування площини АА 1 В і плоскості, що проходить через середини ребер А 1 В 1 , C 1 D 1 , CD.

6) Знайдіть площу перерізу куба площиною, що проходить через ребро ВВ 1 і середину ребра A 1 D 1 (ВВ 1 = а).

7) Побудуйте точку, симетричну точці А щодо площини A1B1C.

424. У правильному тетраедрі АBCD з ребром 2 см точка М - середина DВ, а точка N - середина АС.

1°) Доведіть, що пряма DВ перпендикулярна до площини

2°) Доведіть, що площина ВDМ перпендикулярна до плоскості АМС.

3) Через точку Про перетин медіан трикутника АDС проведіть пряму, перпендикулярну до площини АМС.

4) Знайдіть довжину відрізка цієї прямої всередині тетраедра. 5) У якому відношенні площину АМС поділяє цей відрізок?

425. Два рівносторонні трикутники АВС та ADC лежать у перпендикулярних площинах.

1°) Знайдіть довжину відрізка BD, якщо AC = 1 см.

2) Доведіть, що площина BKD (K лежить на прямій AC ) перпендикулярна до площини кожного з трикутників тоді і тільки тоді, коли K є серединою сторони AC.

426. Прямокутник ABCD, сторони якого 3 см і 4 см, перегнули по діагоналі AC так, що трикутники ABC та ADC розташувалися у перпендикулярних площинах. Визначте відстань між точками B та D після того, як перегнули прямокутник ABCD.

427. Через цю точку проведіть площину, перпендикулярну до кожної з двох даних площин.

428 °. Доведіть, що площини суміжних граней куба перпендикулярні.

429. Площини α та β перпендикулярні між собою. З точки А площини α проведено перпендикулярну площину β прямою АВ. Доведіть, що пряма АВ лежить у площині?

430. Доведіть, що якщо площина і пряма, що не лежить у цій площині, перпендикулярні до однієї і тієї ж площини, то вони паралельні між собою.

431. Через точки А і В , що лежать на лінії перетину р перпендикулярних між собою площин α і β, проведено перпендикулярні р прямі: АА 1 в α, ВВ 1 у β. Точка X лежить на прямій АА 1 , а точка Y - на ВB 1 . Доведіть, що пряма ВB 1 перпендикулярна до прямої ВХ , а пряма АA 1 перпендикулярна до прямої АY.

432*. Через середину кожної сторони трикутника проведена площина перпендикулярна цій стороні. Доведіть, що всі три проведені площини перетинаються однією прямою, перпендикулярною площині трикутника.

Вправи для повторення

433. У рівносторонньому трикутнику зі стороною b визначте: 1) висоту; 2) радіуси вписаного та описаного кіл.

434. З однієї точки проведено до цієї прямої перпендикуляр і дві похилі. Визначте довжину перпендикуляра, якщо похилі дорівнюють 41 см та 50 см, а їх проекції на цю пряму відносяться, як 3:10.

435. Визначте катети прямокутного трикутника, якщо біс- сектриса прямого кута ділить гіпотенузу на відрізки 15 см та

Основне визначення

Дві площини називає-

ються перпендикулярними , якщо кожна з них утворена прямо- ми, перпендикулярні- ми другої площини і проходять через точки перетину цих площин.

	Основні твердження
Ознака перпенді		Якщо одна
кулярності		площин	прохо-
площин		дит через
		перпендикулярну
		другий площині, то		b α, b β α β
		ці площини пер-
		пендикулярні.

		перпен-		дві площини
дикулярі			перпендикулярні, то
перетинуперпен			пряма, належать
дикулярних		плос-	щаюча однієї площини
			та перпендикулярна
				перетину
			цих площин, пер-		α β, b β, c = α ∩β,
			пендикулярна другий		b c b α
			площині.